Amazon
Web Services
Microsoft Azure
Google Cloud PlatformGraph and network analysis on Databricks
This article gives an overview of Databricks capabilities for graph analysis and an introduction to basic graph concepts. Graphs are also commonly called networks, especially in the context of a specific area of study, such as social networks, or communication networks.
A graph is a set of vertices that are connected by edges. Vertices are often also known as nodes, and edges are instead sometimes called links, relationships or arcs. For example, social networks represent the connections between people. Other examples include transportation networks, such as flight, train, or bus connections between cities, and telecommunication networks, such as the cables that carry internet traffic between servers. Graph processing is also commonly used in areas such as fraud or threat detection and product recommendation. Many business problems benefit from an understanding and analysis of networks through graph processing, and it is especially powerful when combined with other analytics techniques, including machine learning.
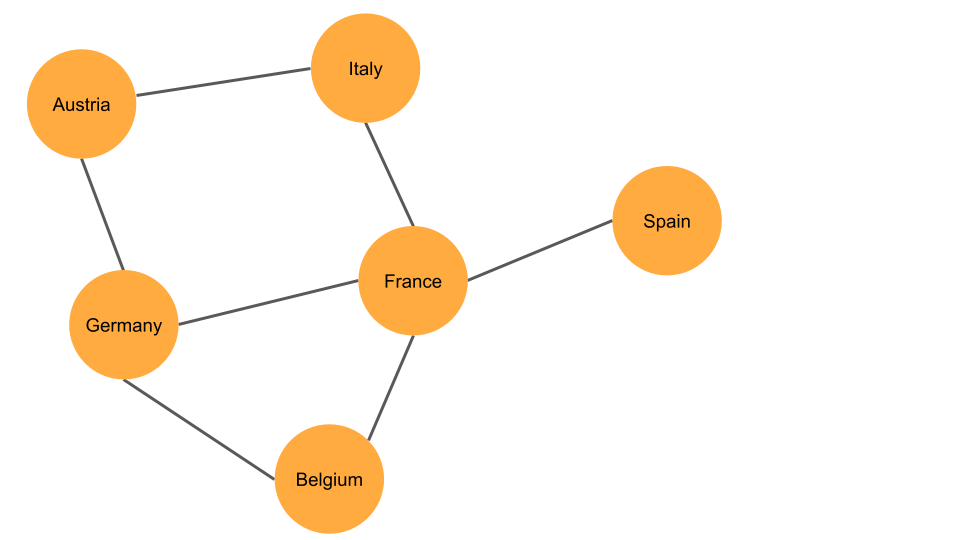
The diagram shows a simple example. The nodes in this network are 6 countries in western and central Europe. The lines, or edges, in the diagram indicate that two countries share a border.
Databricks Runtime ML includes network analysis packages for problems at any scale. For relatively small networks that can be processed on a single compute node, use NetworkX. For large networks that require distributed processing, use GraphFrames. You can also install additional open source packages as needed, or connect to external partners and tools for graph processing and visualization.
The rest of this article describes basic network analysis concepts and includes a notebook that uses the package NetworkX to illustrate some of those concepts.
Graph and network analysis concepts
This section describes some of the basic concepts of network analysis.
Nodes and edges
In network analysis, a network, or graph, consists of a set of nodes and a set of edges, or links, that connect the nodes. Nodes represent the things being connected, such as people or cities. Edges represent the connections or relationships between them, such as people who have worked together, or train stations that have a direct link between them.
Nodes are also called vertices, points, or entities. Edges are also called lines, relationships, or links.
Directed and undirected networks
An edge in a network can represent a one-way relationship, such as a fan following a celebrity on a social network, or a two-way relationship, such as coworkers. If edges can be one-way, the network is called directed. If edges do not have an associated direction, the network is called undirected.
Network and node properties
Shortest path
The shortest path is the minimum distance between two nodes, taking into account directional links and, optionally, edge weights. For example, in the previous diagram, the shortest path between the nodes Germany and Spain is through France, for a path distance of 2.
Centrality
Centrality is a way to measure the importance of a node in a network. There are several different measures of centrality. The degree centrality of a node is based on the fraction of nodes in a network that the node is directly connected to. The betweenness centrality of a node is the fraction of shortest paths in a network that go through the node.
Degree distribution
The degree distribution of a network is the number of nodes of each degree. It provides information about the structure and organization of the network.
Diameter
The diameter of a network is the maximum of the shortest paths between any two nodes. The diameter is equivalent to the maximum eccentricity of nodes in a network.
Density
The density of a graph is the number of edges in the graph divided by the total number of possible edges. For an undirected graph, the total number of possible edges is n(n-1)/2, where n is the number of nodes. For a directed graph, each edge has two possible directions, so the total number of possible edges is n(n-1).
Small-world networks
Most real-world networks are not randomly connected, and instead exhibit some sort of patterns and substructure. An example of such a pattern in networks involving people is the “small-world phenomenon”, by which we observe closely linked subgroups and a short average path length between any two nodes. These patterns are very common in practice, and lead to common issues in graph processing at scale, such as natural occurrences of data skew to contend with when processing large graphs.