Get started as a Databricks Data Science & Engineering user

This tutorial gets you going with Databricks Data Science & Engineering: you create a cluster and a notebook, create a table from a dataset, query the table, and display the query results.

Tip

As a supplement to this article, check out the Quickstart Tutorial notebook, available on your Databricks Data Science & Engineering landing page, for a 5-minute hands-on introduction to Databricks. Simply log in to Databricks and click Explore the Quickstart Tutorial. If you don’t see the tutorial, select Data Science & Engineering from the persona switcher in the sidebar.

Requirements

You are logged into Databricks, and you’re in the Data Science & Engineering workspace. See Sign up for a Databricks free trial.

Step 1: Orient yourself to the Databricks Data Science & Engineering UI

Landing page

From the sidebar at the left and the Common Tasks list on the landing page, you access fundamental Databricks Data Science & Engineering entities: the Workspace, clusters, tables, notebooks, jobs, and libraries. The Workspace is the special root folder that stores your Databricks assets, such as notebooks and libraries, and the data that you import.

Use the sidebar

You can access all of your Databricks assets using the sidebar. The sidebar’s contents depend on the selected persona: Data Science & Engineering, Machine Learning, or SQL.

  • By default, the sidebar appears in a collapsed state and only the icons are visible. Move your cursor over the sidebar to expand to the full view.

  • To change the persona, click the icon below the Databricks logo Databricks logo, and select a persona.

    change persona

  • To pin a persona so that it appears the next time you log in, click pin persona next to the persona. Click it again to remove the pin.

  • Use Menu options at the bottom of the sidebar to set the sidebar mode to Auto (default behavior), Expand, or Collapse.

  • When you open a machine learning-related page, the persona automatically switches to Machine Learning.

Get help

To get help, click Help icon Help in the lower left corner.

Help menu

Step 2: Create a cluster

A cluster is a collection of Databricks computation resources. To create a cluster:

  1. In the sidebar, click compute icon Compute.

  2. On the Compute page, click Create Cluster.

    Create cluster

  3. On the Create Cluster page, specify the cluster name Quickstart and select 7.3 LTS (Scala 2.12, Spark 3.0.1) in the Databricks Runtime Version drop-down.

  4. Click Create Cluster.

Step 3: Create a notebook

A notebook is a collection of cells that run computations on an Apache Spark cluster. To create a notebook in the Workspace:

  1. In the sidebar, click Workspace Icon Workspace.

  2. In the Workspace folder, select Down Caret Create > Notebook.

    Create notebook

  3. On the Create Notebook dialog, enter a name and select SQL in the Language drop-down. This selection determines the default language of the notebook.

  4. Click Create. The notebook opens with an empty cell at the top.

Step 4: Create a table

Create a table using data from a sample CSV data file available in Databricks datasets, a collection of datasets mounted to Databricks File System (DBFS), a distributed file system installed on Databricks clusters. You have two options for creating the table.

Option 1: Create a Spark table from the CSV data

Use this option if you want to get going quickly, and you only need standard levels of performance. Copy and paste this code snippet into a notebook cell:

DROP TABLE IF EXISTS diamonds;

CREATE TABLE diamonds USING CSV OPTIONS (path "/databricks-datasets/Rdatasets/data-001/csv/ggplot2/diamonds.csv", header "true")

Option 2: Write the CSV data to Delta Lake format and create a Delta table

Delta Lake offers a powerful transactional storage layer that enables fast reads and other benefits. Delta Lake format consists of Parquet files plus a transaction log. Use this option to get the best performance on future operations on the table.

  1. Read the CSV data into a DataFrame and write out in Delta Lake format. This command uses a Python language magic command, which allows you to interleave commands in languages other than the notebook default language (SQL). Copy and paste this code snippet into a notebook cell:

    %python

diamonds = spark.read.csv("/databricks-datasets/Rdatasets/data-001/csv/ggplot2/diamonds.csv", header="true", inferSchema="true")
diamonds.write.format("delta").save("/mnt/delta/diamonds")

  2. Create a Delta table at the stored location. Copy and paste this code snippet into a notebook cell:

    DROP TABLE IF EXISTS diamonds;

CREATE TABLE diamonds USING DELTA LOCATION '/mnt/delta/diamonds/'

Run cells by pressing SHIFT + ENTER. The notebook automatically attaches to the cluster you created in Step 2 and runs the command in the cell.

Step 5: Query the table

Run a SQL statement to query the table for the average diamond price by color.

  1. To add a cell to the notebook, mouse over the cell bottom and click the Add Cell icon.

    Add cell

  2. Copy this snippet and paste it in the cell.

    SELECT color, avg(price) AS price FROM diamonds GROUP BY color ORDER BY COLOR

  3. Press SHIFT + ENTER. The notebook displays a table of diamond color and average price.

    Run command

Step 6: Display the data

Display a chart of the average diamond price by color.

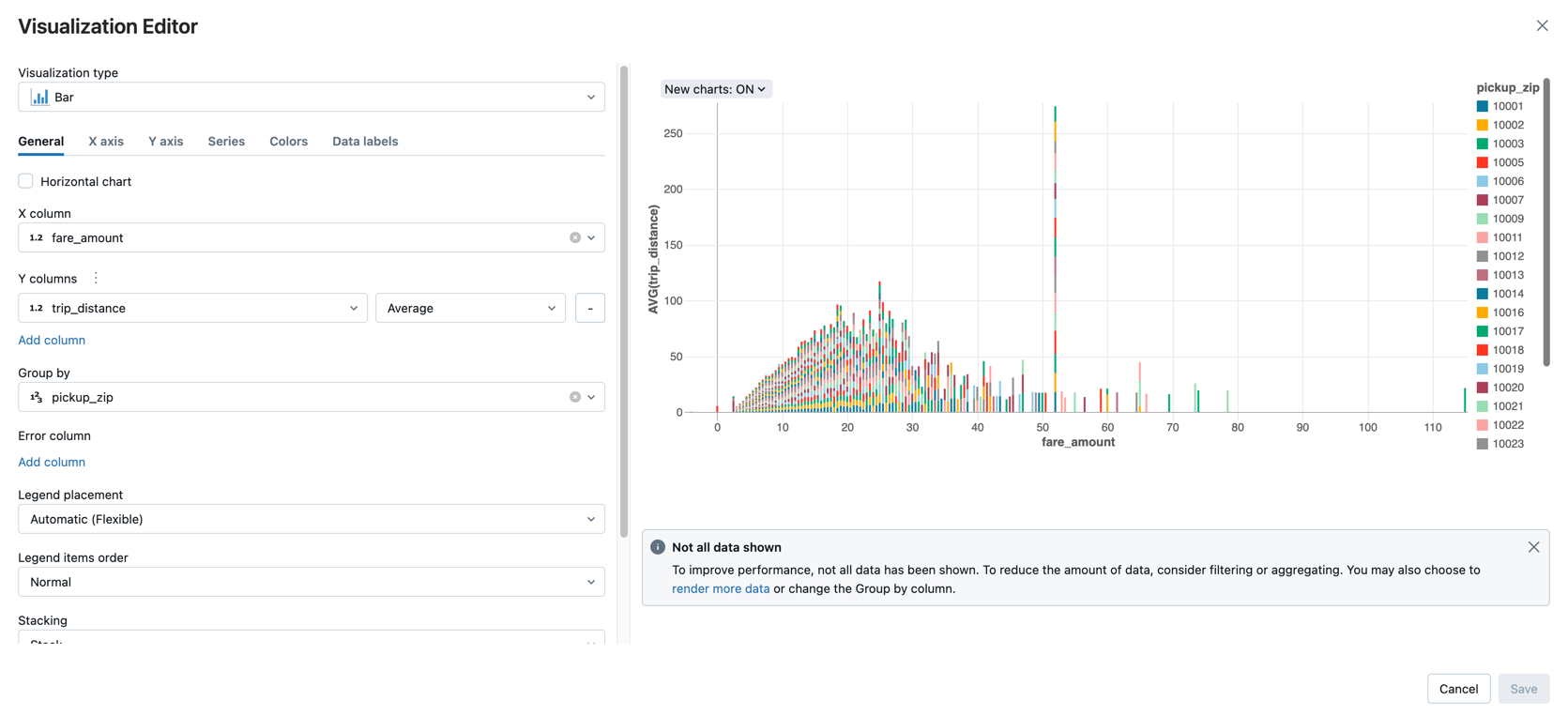
  1. Click the Bar chart icon Chart Button.

  2. Click Plot Options.

    • Drag color into the Keys box.

    • Drag price into the Values box.

    • In the Aggregation drop-down, select AVG.

      Select aggregation

  3. Click Apply to display the bar chart.

    Apply chart type

What’s next

We’ve now covered the basics of Databricks Data Science & Engineering, including creating a cluster and a notebook, running SQL commands in the notebook, and displaying results.