Databricks でのグラフとネットワーク分析
この記事では、グラフ分析のための Databricks 機能の概要と、グラフの基本的な概念の概要について説明します。 グラフは、特にソーシャルネットワークや通信ネットワークなど、特定の研究分野の文脈では、一般にネットワークとも呼ばれます。
グラフは、エッジによって接続された頂点のセットです。 頂点はノードとも呼ばれ、エッジはリンク、リレーションシップ、またはアークと呼ばれることもあります。 たとえば、ソーシャルネットワークは人々の間のつながりを表しています。 その他の例としては、都市間のフライト、電車、バスの接続などの交通ネットワークや、サーバー間でインターネット トラフィックを伝送するケーブルなどのテレコミュニケーション ネットワークなどがあります。 グラフ処理は、詐欺や脅威の検出、製品の推奨などの分野でも一般的に使用されます。 多くのビジネス上の問題は、グラフ処理によるネットワークの理解と分析から恩恵を受けており、機械学習などの他のアナリティクス手法と組み合わせると特に強力です。
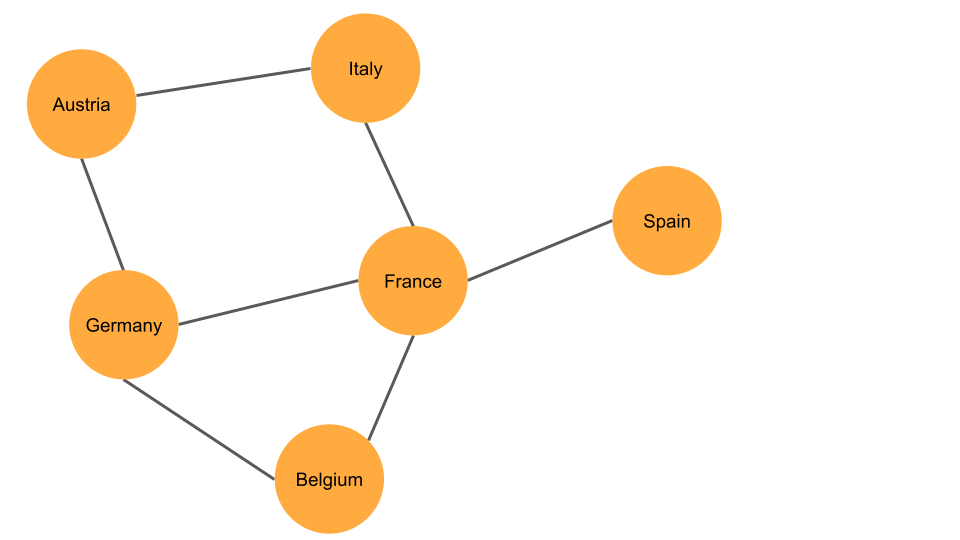
この図は簡単な例を示しています。 このネットワークのノードは、西ヨーロッパと中央ヨーロッパの6か国です。 図の線 (エッジ) は、2 つの国が国境を共有していることを示しています。
Databricks Runtime ML には、あらゆる規模の問題に対応するネットワーク分析パッケージが含まれています。 1 つのコンピュート ノードで処理できる比較的小規模なネットワークの場合は、 NetworkX を使用します。 分散処理が必要な大規模なネットワークの場合は、 GraphFrames を使用します。 また、必要に応じて追加のオープンソースパッケージをインストールしたり、グラフの処理や視覚化のために外部のパートナーやツールに接続したりすることもできます。
この記事の残りの部分では、ネットワーク分析の基本的な概念について説明し、NetworkX パッケージを使用してそれらの概念の一部を説明するノートブックが含まれています。
グラフ解析とネットワーク解析の概念
このセクションでは、ネットワーク解析の基本概念の一部について説明します。
ノードとエッジ
ネットワーク解析では、ネットワーク(グラフ)は、ノードのセットと、ノードを接続するエッジ(リンク)のセットで構成されます。 ノードは、人や都市など、接続されているものを表します。 エッジは、一緒に働いた人々や、エッジ間に直接リンクしている駅など、エッジ間の接続または関係を表します。
ノードは、頂点、点、またはエンティティとも呼ばれます。 エッジは、ライン、リレーションシップ、またはリンクとも呼ばれます。
有向ネットワークと無向ネットワーク
ネットワーク内のエッジは、ソーシャル ネットワークで有名人をフォローするファンなどの一方向の関係や、同僚などの双方向の関係を表すことができます。 エッジが一方向である場合、ネットワークは指向性と呼ばれます。 エッジに方向が関連付けられていない場合、ネットワークは無向と呼ばれます。
ウェイト エッジ
エッジにはウェイトを付けることができます。 ネットワーク内のウェイトの例としては、高速道路やケーブルの収容力などがあります。
度
ノードの次数は、ノードにリンクするエッジの数です。 たとえば、前の図では、ノード "France" の次数は 4 です。
有向グラフの場合、次数内はノードに入るエッジの数で、次数外はノードから離れるエッジの数です。
ネットワークとノードのプロパティ
最短パス
最短パスは、2 つのノード間の最小距離であり、アカウント 方向リンクと、オプションでエッジの重みを考慮します。 たとえば、前の図では、ノード Germany と Spain の間の最短パスはフランスを経由し、パス距離は 2 です。
中心
中心性は、ネットワーク内のノードの重要性を測定する方法です。 中心性にはいくつかの異なる尺度があります。 ノードの次数中心性は、ノードが直接接続されているネットワーク内のノードの割合に基づいています。 ノードの媒介中心性は、ノードを通過するネットワーク内の最短パスの割合です。
学位分布
ネットワークの次数分布は、各次数のノード数です。 ネットワークの構造と組織に関する情報を提供します。
直径
ネットワークの直径は、任意の 2 つのノード間の最短パスの最大値です。 直径は、ネットワーク内のノードの最大偏心に相当します。
密度
グラフの密度は、グラフ内のエッジの数を可能なエッジの総数で割った値です。 無向グラフの場合、可能なエッジの総数は n(n-1)/2 で、n はノードの数です。 有向グラフの場合、各エッジには2つの可能な方向があるため、可能なエッジの総数はn(n-1)です。
スモールワールドネットワーク
ほとんどの現実世界のネットワークはランダムにつながっているわけではなく、何らかのパターンと下部構造を示しています。 このようなパターンの例として、人が関わるネットワークには「スモールワールド現象」があり、これにより、密接にリンクされたサブグループと、任意の2つのノード間の平均経路長が短いことが観察されます。 これらのパターンは実際には非常に一般的であり、大規模なグラフを処理するときに自然に発生するデータ スキューなど、大規模なグラフ処理で一般的な問題を引き起こします。
ノートブックの例
次のノートブック例では、Databricks Runtime for ML に組み込まれている NetworkX パッケージを使用して、いくつかの基本的なネットワーク分析の概念を示しています。